无向图的 DFS 生成树
若有一张图 DFS 的结果如下,其中黑色边表示 DFS 过程中走的边,灰色表示未走的边。
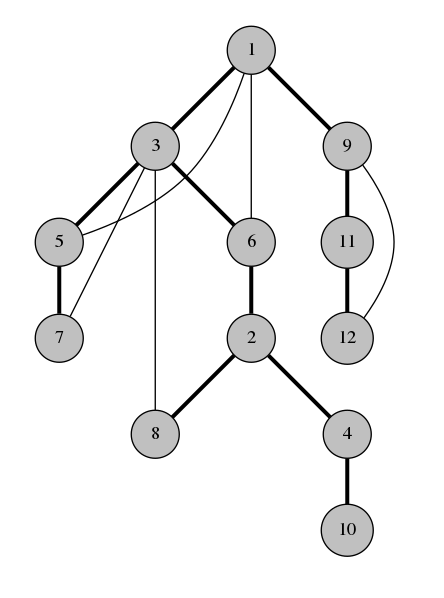
称如 $(1,3)$,DFS 经过的边为树边(span-edge),如 $(5,1)$ 连接一个点及其祖先的非树边为返祖边(back-edge)。本图只存在这两种边,且并非偶然。记连接生成树中旁系亲属的边为横叉边(cross-edge),则它在图中不会存在。证明如下:
若有一条边 $(u,v)$,在探索到 $u$ 时 $v$ 尚未探索,则 $(u,v)$ 为非树边等价于探索 $u$ 其他子节点时访问到了 $v$,$u$ 和 $v$ 满足祖先关系。
这是无向图 DFS 生成树一个重要性质。
找桥
返祖边不可能是桥,因为仅保留树边的生成树就足以保证连通。
若树边 $(u,v)$ 是桥,将原图分成两个不连通的部分,则其中一个为以 $v$ 为根的子树,子树中连接的最低深度的返祖边不能连通到 $u$ 或 $u$ 的祖先。基于这一个要求,就有通行的实现方法,记录所有子树的 $low$。
将无向图定向生成强联通分量
若存在割边则一定无解。
否则直接对其 DFS,将树边从父到子定向,返祖边从子到祖先定向,即可得到一组解。
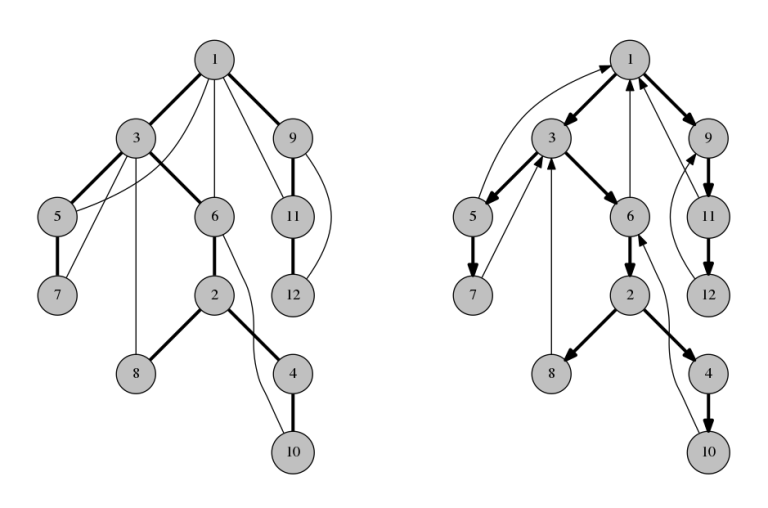
考虑证明这个事实。
对于每个点可以沿树边通向子树中节点。则返祖边若从上到下定向是无意义的,从子到祖先定向不会更劣,也就是说这种定向可以蕴含其他任意方案。对于每一个节点,一定可以到达它的父亲,否则连向其父亲的树边就是割边了,重复这一过程,则可以到达任意祖先。
找环
点仙人掌是每个点最多属于一个简单环的简单连通图。在这上面解决问题通常需要将环提取出。
生成树一定不存在环,而每一个条返祖边都一定会生成一个环。基于这个事实,可以让找环的过程简单。
删边生成二分图
这是上面技巧的一个应用。
一张图是二分图等价于这张图不存在奇环。所以被删除的边一定要破坏所有奇环,即位于所有奇环的交。
找这种边,相当于 DFS 到一个生成奇环的返祖边 $(u,v)$ 时,将 $u$ 到 $v$ 的路径上的边的覆盖次数 $+1$。最终符合要求的边的覆盖次数等于奇环个数。既然是返祖边,就可以简单的树上差分。
有向图的 DFS
与无向图不同,结果中可能会存在横叉边。有向图上的 DFS 可以用于构造支配树。
树的 DFS 序
树的一个子树的 DFS 序是连续的,可以对每个子树求出 DFS 开始值和结束位置,将子树限制变成区间限制。
CF620E New Year Tree
相对暴力的,查询时可以枚举每一个颜色在子树中是否出现,利用 DFS 序连续的性质可以使用树状数组记录。对于本题,可以以损失可减性的代价,将所有颜色压到一个 long long 里,换为线段树即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 400010;
vector <int> g[N];
int pos[N], to[N];
int kw = 0, w[N];
void dfs(int v, int pr) {
pos[v] = kw;
w[kw++] = v;
for (int j = 0; j < (int) g[v].size(); j++) {
int u = g[v][j];
if (u != pr) {
dfs(u, v);
}
}
to[v] = kw - 1;
}
long long a[4 * N];
bool put[4 * N];
int color[N];
void build(int x, int l, int r) {
if (l < r) {
int y = (l + r) >> 1;
build(x + x, l, y);
build(x + x + 1, y + 1, r);
a[x] = a[x + x] | a[x + x + 1];
put[x] = false;
} else {
a[x] = 1LL << color[w[l]];
put[x] = true;
}
}
inline void push(int x) {
if (put[x]) {
a[x + x] = a[x + x + 1] = a[x];
put[x + x] = put[x + x + 1] = true;
put[x] = false;
}
}
inline void gather(int x) {
a[x] = a[x + x] | a[x + x + 1];
}
void modify(int x, int l, int r, int ll, int rr, long long v) {
if (r < ll || rr < l) {
return;
}
if (ll <= l && r <= rr) {
a[x] = v;
put[x] = true;
return;
}
push(x);
int y = (l + r) >> 1;
modify(x + x, l, y, ll, rr, v);
modify(x + x + 1, y + 1, r, ll, rr, v);
gather(x);
}
long long get(int x, int l, int r, int ll, int rr) {
if (r < ll || rr < l) {
return 0;
}
if (ll <= l && r <= rr) {
return a[x];
}
push(x);
int y = (l + r) >> 1;
long long res = get(x + x, l, y, ll, rr);
res |= get(x + x + 1, y + 1, r, ll, rr);
gather(x);
return res;
}
int main() {
int n, m;
scanf("%d %d", &n, &m);
for (int i = 0; i < n; i++) {
scanf("%d", color + i);
}
for (int i = 0; i < n; i++) {
g[i].clear();
}
for (int i = 0; i < n - 1; i++) {
int foo, bar;
scanf("%d %d", &foo, &bar);
foo--; bar--;
g[foo].push_back(bar);
g[bar].push_back(foo);
}
dfs(0, -1);
build(1, 0, n - 1);
while (m--) {
int type;
scanf("%d", &type);
if (type == 1) {
int foo, bar;
scanf("%d %d", &foo, &bar);
foo--;
modify(1, 0, n - 1, pos[foo], to[foo], 1LL << bar);
} else {
int foo;
scanf("%d", &foo);
foo--;
long long value = get(1, 0, n - 1, pos[foo], to[foo]);
printf("%d\n", __builtin_popcountll(value));
}
}
return 0;
// tourist
CF856D Masha and Cactus
构成仙人掌的条件相当于加入边 $(u,v)$ 时,给树上 $u$ 到 $v$ 的路径染色,且每个点最多被染色一次。可以想到树上 DP,对于每个位置只考虑 $lca$ 为这个点的待加入边,若不选择一条加入,则 $f_x=\sum_{v\in son_x}{f_v}$。若选择加入某个边,则分析子树去除这条链的形状,剖分出了链上每一个点的子树,$f_x=\sum_{v\in 剩下的子树}{f_v}$。既然子树是围绕链展开的,考虑只使用当前点和链上的信息表示,可以差分地用 $g_x=-f_x+\sum_{v\in son_x}f_v$,则 $\sum_{v\in 剩下的子树}{f_x}=\sum_{i\in son_x}{f_i}+\sum_{i\in 链}{g_i}$。对其再一次使用差分,记 $h_u$ 为从 $u$ 到根路径上的 $\sum{g}$,则上式还可以写成 $\sum_{i\in son_x}{f_i}+h_u+h_v-2h_x$。可以在 DFS 过程中动态维护 $h$,处理完某一个点后将这个子树每一点的 $h$ 加上 $g_x$。使用 DFS 序即可简单维护。
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
constexpr int maxn = 200000 + 10;
vector<int> G[maxn];
int dep[maxn], dfn[maxn], ed[maxn], cnt;
int st[18][maxn], fa[maxn];
#define get(x, y) (dep[x] < dep[y] ? (x) : (y))
int lca(int u, int v)
{
u = dfn[u]; v = dfn[v];
if (u > v) swap(u, v);
int k = 31 ^ __builtin_clz(v - u);
return fa[get(st[k][u + 1], st[k][v - (1 << k) + 1])];
}
int t[maxn];
#define lowbit(x) ((x) &- (x))
void add(int x, int y)
{
if (x) for (; x<maxn; x+=lowbit(x))
t[x] += y;
}
int query(int x)
{
int y = 0;
for (; x; x-=lowbit(x)) y += t[x];
return y;
}
void dfs(int u)
{
st[0][dfn[u] = ++cnt] = u;
for (int v : G[u]) fa[v] = u, dep[v] = u, dfs(v);
ed[u] = cnt;
}
int u[maxn], v[maxn], w[maxn];
vector<int> c[maxn];
int f[maxn];
void dp(int u)
{
int s = 0;
for (int v : G[u]) dp(v), s += f[v];
f[u] = s;
for (int i : c[u])
f[u] = max(f[u], s + query(dfn[::u[i]]) + query(dfn[v[i]]) + w[i]);
add(dfn[u], s - f[u]);
add(ed[u] + 1, f[u] - s);
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n, m;
cin >> n >> m;
for (int i=2;i<=n;++i)
{
int u;
cin >> u;
G[u].emplace_back(i);
}
dfs(1);
for (int i=1;i<18;++i)
for (int j=1;j+(1<<i)-1<=n;++j)
st[i][j] = get(st[i-1][j], st[i-1][j+(1<<(i-1))]);
for (int i=1;i<=m;++i)
{
cin >> u[i] >> v[i] >> w[i];
c[lca(u[i], v[i])].emplace_back(i);
}
dp(1);
cout << f[1] << endl;
return 0;
}
CF246E Blood Cousins Return
可以将询问离线,在 DFS 过程中求解。对于每个子树,询问的区别仅在于目标的深度。使用 map<int, set<int> > 记录当前子树每个深度的颜色种类,对于某个子树 $u$,先将点 $u$ 插入。递归完某一个子节点 $v$ 后,比较子树 $v$ 和 $u$ 当前的大小关系启发式合并。
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
constexpr int maxn = 100000 + 10;
map<string, int> mp;
int idx;
int d[maxn], ans[maxn];
vector<int> G[maxn], q[maxn];
map<int, set<int> > f[maxn];
using pii = pair<int, int>;
vector<pii> st[maxn];
int dep[maxn], a[maxn];
void dfs(int u, int fa)
{
dep[u] = dep[fa] + 1;
for (int v : G[u]) dfs(v, u);
}
void solve(int u, int fa)
{
st[u].emplace_back(pii(dep[u], a[u]));
f[u][dep[u]].insert(a[u]);
for (int v : G[u])
{
if (v == fa) continue;
solve(v, u);
if (st[v].size() > st[u].size()) swap(st[v], st[u]), swap(f[u], f[v]);
for (auto i : st[v])
st[u].emplace_back(i), f[u][i.first].insert(i.second);
}
for (int i : q[u]) ans[i] = f[u][d[i]].size();
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
for (int i=1;i<=n;++i)
{
string s;
int x;
cin >> s >> x;
if (mp.find(s) == mp.end()) mp[s] = ++idx;
a[i] = mp[s];
G[x].emplace_back(i);
}
dfs(0, 0);
int m;
cin >> m;
for (int i=1;i<=m;++i)
{
int x, k;
cin >> x >> k;
q[x].emplace_back(i);
d[i] = dep[x] + k;
}
solve(0, 0);
for (int i=1;i<=m;++i) cout << ans[i] << '\n';
return 0;
}
CF893F Subtree Minimum Query
若没有深度限制,则可以通过 DFS 序将问题转化为区间 $\min$。加上深度限制后,显然有按照深度为第一维,DFS 序为第二位建树套树的 $2\log$ 做法。但是若确定了 DFS 序的区间,就已经有了其深度下界,所以可以将第一维的线段树变成前缀和,主席树即可单 $\log$。
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
constexpr int maxn = 100000 + 10;
struct node
{
int s = 0x3f3f3f3f, l, r;
} t[maxn << 6];
void push(int rt)
{
t[rt].s = min(t[t[rt].l].s, t[t[rt].r].s);
}
int tot;
void update(int& o, int rt, int l, int r, int k, int x)
{
t[o = ++tot] = t[rt];
if (l == r) return t[o].s = min(t[o].s, x), void();
int mid = (l + r) >> 1;
if (k <= mid) update(t[o].l, t[rt].l, l, mid, k, x);
else update(t[o].r, t[rt].r, mid + 1, r, k, x);
push(o);
}
int query(int o, int l, int r, int L, int R)
{
int mid = (l + r) >> 1, ans = 0x3f3f3f3f;
if (!o) return ans;
if (L <= l && r <= R) return t[o].s;
if (L <= mid) ans = query(t[o].l, l, mid, L, R);
if (mid < R) ans = min(ans, query(t[o].r, mid + 1, r, L, R));
return ans;
}
vector<int> G[maxn];
int dfn[maxn], ed[maxn];
int cnt;
vector<int> c[maxn];
int a[maxn];
int dep[maxn];
void dfs(int u, int fa)
{
c[dep[u] = dep[fa] + 1].emplace_back(u);
dfn[u] = ++cnt;
for (int v : G[u]) if (v != fa) dfs(v, u);
ed[u] = cnt;
}
int rt[maxn];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n, m, r;
cin >> n >> r;
for (int i=1;i<=n;++i) cin >> a[i];
for (int i=1;i<n;++i)
{
int u, v;
cin >> u >> v;
G[u].emplace_back(v);
G[v].emplace_back(u);
}
dfs(r, 0);
for (int i=1;i<=n;++i)
{
rt[i] = rt[i - 1];
for (int j : c[i]) update(rt[i], rt[i], 1, n, dfn[j], a[j]);
}
cin >> m;
int lst = 0;
while (m--)
{
int x, k;
cin >> x >> k;
x = (x + lst) % n + 1;
k = (k + lst) % n;
cout << (lst = query(rt[min(n, dep[x] + k)], 1, n, dfn[x], ed[x])) << '\n';
}
return 0;
}
CF276E Little Girl and Problem on Trees
细节题。题目保证形态为根下面挂载了一些链,则可以对于每个链建一个以深度为下标的树状数组,另外开一个公用的树状数组。每个修改都要考虑当前链的靠近点,以及先走若干步到达根,并用剩余步数到达任意链深度较浅的一些点。核心代码是极短的。
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
constexpr int maxn = 100000 + 10;
struct bit
{
vector<i64> t;
#define lowbit(x) ((x) &- (x))
void add(int x, int y)
{
if (x >= t.size()) return;
if (x) for (; x<t.size(); x+=lowbit(x))
t[x] += y;
}
int query(int x)
{
if (x >= t.size()) return 0;
i64 y = 0;
for (; x; x-=lowbit(x)) y += t[x];
return y;
}
void init(int x)
{
t.resize(x + 7);
}
} t[maxn], g;
int id[maxn];
int dep[maxn];
vector<int> G[maxn];
void dfs(int u, int fa, int p)
{
id[u] = p;
dep[u] = dep[fa] + 1;
t[p].init(dep[u]);
for (int v : G[u])
if (v != fa) dfs(v, u, p);
}
i64 s[maxn];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n, m;
cin >> n >> m;
for (int i=1;i<n;++i)
{
int u, v;
cin >> u >> v;
G[u].emplace_back(v);
G[v].emplace_back(u);
}
int c = 0;
dep[1] = 1;
for (int v : G[1]) dfs(v, 1, ++c);
g.init(n);
i64 tot = 0;
while (m--)
{
int o;
cin >> o;
if (o == 1)
{
int u;
cin >> u;
s[0] = 0;
cout << s[id[u]] + tot + g.query(dep[u]) + t[id[u]].query(dep[u]) << '\n';
}
else
{
int u, x, d;
cin >> u >> x >> d;
if (d >= dep[u] - 1)
{
tot += x;
g.add(d - dep[u] + 3, -x);
s[id[u]] -= x;
t[id[u]].add(d - dep[u] + 3, x);
}
t[id[u]].add(max(1, dep[u] - d), x);
t[id[u]].add(dep[u] + d + 1, -x);
}
}
return 0;
}
